- Modules
- Master Controllers
- Applying the Coordinates of a Master Controller Widget to Deformers
Applying the Coordinates of a Master Controller Widget to Deformers
T-HSCP-002-012
It is possible to use Master Controller widgets to apply transformations to deformers. However, before attempting that, it is important to understand the difference between deformations that have absolute attributes and the ones that have relative attributes.
When using the Rigging tool to create Bone, Game Bone and Curve transformation chains, Harmony creates each deformation node with the attribute "Apply Parent Transformation" enabled. This attribute makes it so each point is deformed by their parent—the previous point in the chain—before they apply their own deformations to the drawing. This makes manipulating these types of deformation points difficult as their deformation matrices are not fully reversible.
Hence, using a Master Controller widget to manipulate deformers is more easily achieved with Envelope type deformations. The Rigging tool creates Curve deformation nodes with the attribute "Apply Parent Transformation" disabled. This means envelope deformation points are not affected by their parent's deformations. Therefore, the deformation matrix for all the points in a Curve deformation chain is the same, that is, the one carried by the parent of the chain's offset, which would typically be a peg or a drawing node, and would hence be fully reversible. The process then becomes similar to when a widget is used to manipulate pegs or elements.
With the inverse matrix of a deformation node, we can convert world coordinates to a deformation node's coordinates system. However, it is important to understand that curve and envelope deformation nodes are represented by three points: The central point, and the two tangent points defining the secondary points of the Bezier curves. If you plan to change the position of a curve or envelope deformation node, you will also need to modify its tangent positions, with an algorithm such as:
Tangent0 in fields = Previous-Offset + rotation(Vector(length0 * 0.1, 0), orientation0 degrees) Tangent1 = Offset + rotation(Vector(length1 * 0.1, 0), orientation1 degrees)
In the Harmony scripting interface, this would be expressed like so:
var t0FldU = add(previousDeformationNode.fieldOffset, rotate(Point2d(deformationNode.length0 * 0.1, 0), deformationNode.orientation0));
var t1FldU = add(p1FieldUndeformed, rotate(Point2d(deformationNode.length1 * 0.1, 0), 180 + deformationNode.orientation1));
In this example, the deformationNode and previousDeformationNode are Deformation type objects defined as:
function Deformation (nodePath)
{
var currentFrame = frame.current();
this.fieldOffset = node.getAttr(nodePath, currentFrame, "offset").pos2dValue();
this.OGLOffset = scene.toOGL(this.fieldOffset);
this.nodePath = nodePath;
this.nodeType = node.type(nodePath);
if(this.nodeType == "OffsetModule")
{
this.orientation0 = node.getAttr(nodePath, currentFrame, "orientation").doubleValue();
this.orientation1 = 0;
this.length0 = 0;
this.length1 = 0;
}
if(this.nodeType == "CurveModule")
{
this.orientation0 = node.getAttr(nodePath, currentFrame, "orientation0").doubleValue();
this.orientation1 = node.getAttr(nodePath, currentFrame, "orientation1").doubleValue();
this.length0 = node.getAttr(nodePath, currentFrame, "length0").doubleValue();
this.length1 = node.getAttr(nodePath, currentFrame, "length1").doubleValue();
}
}
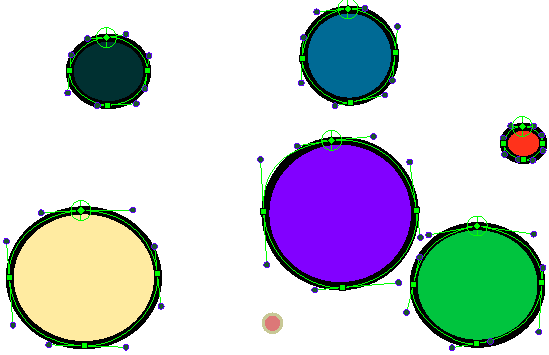
In the following example, we use a Point2dWidget to move the position of envelope deformation nodes towards it proportionally to the inverse distance between those two points. As the user drags the widget around the stage, the deformation points will inch towards it:
This is the node system for this example:
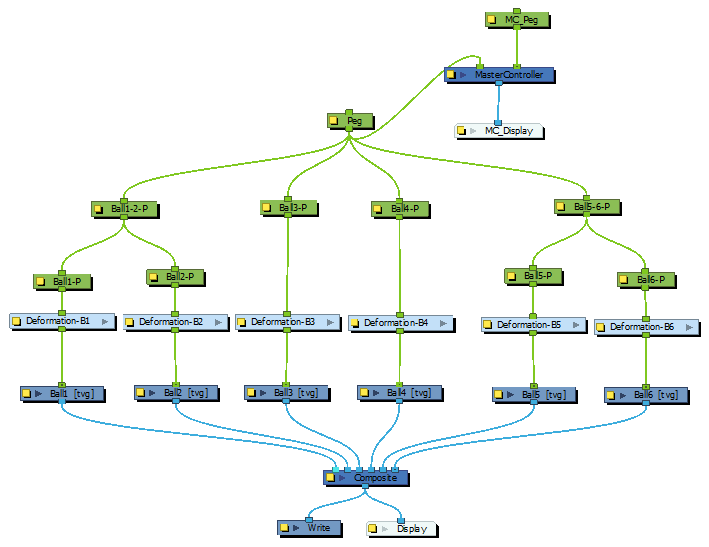
First, we calculate the position of the Point2dWidget in the coordinates system of each parent peg of each deformation group in the scene.
// Get the deformation chains
getDeformationChains(leftmostParent, deformationChains);
for(var i=0; i<deformationChains.length; ++i)
{
// The first node of a deformation chain is always an Offset in our case.
// Convert the position from world coordinates to the target peg
// model coordinates.
// Apply the inverse of the peg parent node transformation to the
// world position to go from world coordinates to (the peg) model
// coordinates
var pegParentNode = node.srcNode(node.parentNode(deformationChains[i][0].nodePath), 0);
var pegParentTransformation = node.getMatrix(pegParentNode, frame.current());
var inversePegTransformation = pegParentTransformation.getInverse();
var pegModelPoint = inversePegTransformation.multiply(worldPoint);
// A deformation chain is simply an array of deformation node parameters.
var deformationChain = deformationChains[i];
if(deformationChain.length == 0)
continue;
// Apply the magnet translation for the deformation node offset and
// both tangent points.
// The first node is the Offset which doesn’t require a previous position.
moveDeformationNode(deformationChain[0], new Deformation(""), pegModelPoint);
for(var j=1; j<deformationChain.length; ++j)
{
moveDeformationNode(deformationChain[j], deformationChain[j-1], pegModelPoint);
}
}
Then, we compute the new position of the offset and tangent points of the deformation chains. We must also compute new orientation values from the new tangent point positions.
function moveDeformationNode(deformationNode, previousDeformationNode, magnetPoint)
{
if(deformationNode.nodeType == "OffsetModule")
{
var p1FieldDeformed = scene.fromOGL(computePosition(magnetPoint, deformationNode.OGLOffset));
node.setTextAttr(deformationNode.nodePath, "offset.X", frame.current(), p1FieldDeformed.x);
node.setTextAttr(deformationNode.nodePath, "offset.Y", frame.current(), p1FieldDeformed.y);
}
else if(deformationNode.nodeType == "CurveModule")
{
// Compute the new Offset attribute position
var p1FieldUndeformed = deformationNode.fieldOffset;
var p1FieldDeformed = scene.fromOGL(computePosition(magnetPoint, deformationNode.OGLOffset));
// Set the new Offset attribute values.
node.setTextAttr(deformationNode.nodePath, "offset.X", frame.current(), p1FieldDeformed.x);
node.setTextAttr(deformationNode.nodePath, "offset.Y", frame.current(), p1FieldDeformed.y);
// Compute the Tangent 0 position
var t0FldU = add(previousDeformationNode.fieldOffset,rotate(Point2d(deformationNode.length0*0.1,0),deformationNode.orientation0));
var t0OGLU = scene.toOGL(t0FldU);
// Compute the new Tangent 0 position
var t0FldD = scene.fromOGL(computePosition(magnetPoint, t0OGLU));
// To compute the new orientation 0 position,
// compute the new position of the previous node.
var p0FieldDeformed = scene.fromOGL(computePosition(magnetPoint, previousDeformationNode.OGLOffset));
// Compute the inverse of the tangent calculation
// to get the new orientation 0 position
var vRef0 = Point2d(1,0);
var ori0D = -angleDelta(minus(toPoint2d(t0FldD),p0FieldDeformed),vRef0);
// Compute the Tangent 1 position
var t1FldU = add(p1FieldUndeformed,rotate(Point2d(deformationNode.length1*0.1,0),180+deformationNode.orientation1));
var t1OGLU = scene.toOGL(t1FldU);
// Compute the new Tangent 1 position
var t1FldD = scene.fromOGL(computePosition(magnetPoint, t1OGLU));
// Compute the inverse of the tangent calculation
// to get the new orientation 1 position
var vRef1 = Point2d(-1,0);
var ori1D = -angleDelta(minus(toPoint2d(t1FldD),p1FieldDeformed),vRef1);
// Set the new orientation attribute values.
node.setTextAttr(deformationNode.nodePath, "orientation0", frame.current(), ori0D);
node.setTextAttr(deformationNode.nodePath, "orientation1", frame.current(), ori1D);
}
}
Time Estimated 25 mins
Difficulty Level Advanced
Topics List
- Introduction to Master Controllers
- Creating a Master Controller
- Creating Master Controller Widgets
- Setting the Properties of a Master Controller Widget
- Updating an Element's Attribute when Manipulating a Master Controller Widget
- Linking Attributes Between Master Controller Widgets
- Updating the Attributes of a Master Controller Widget
- Connecting Master Controller Widgets to Nodes
- Applying the Coordinates of a Master Controller Widget to Nodes
- Applying the Coordinates of a Master Controller Widget to Deformers
- Controlling Nodes Connected to a Master Controller
- Referring to the Master Controller Node
- Master Controllers Examples